BP算法简述
Backpropagation算法
人工智能发展简述
1956年夏,麦卡锡、明斯基提出AI的概念
人工智能是研究开发能够模拟、延伸和扩展人类智能的理论、方法、技术及应用系统的一门新的技术科学,研究目的是促使智能机器会听(语音识别、机器翻译等)、会看(图像识别、文字识别等)、会说(语音合成、人机对话等)、会思考(人机对弈、定理证明等)、会学习(机器学习、知识表示等)、会行动(机器人、自动驾驶汽车等)
起步:1956年—20世纪60年代初
反思:20世纪60年代—70年代初
应用:20世纪70年代初—80年代中
低迷:20世纪80年代中—90年代中
稳步:20世纪90年代中—2010年
蓬勃:2011年至今
专用智能向通用智能发展
人工智能向人机混合智能发展
人工+智能向自主智能发展
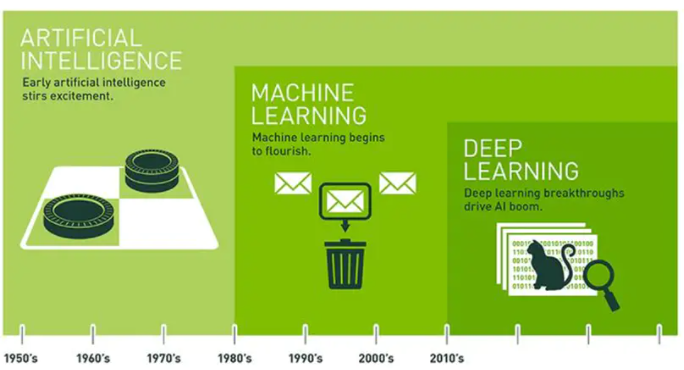
BP算法发展简述
https://blog.csdn.net/jinking01/article/details/103344186
1943年神经元M-P模型
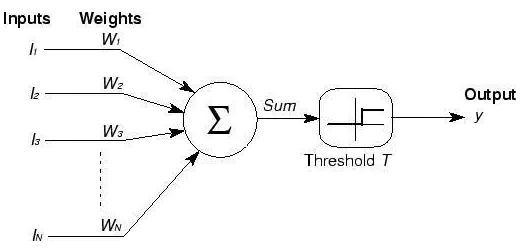
20世纪40年代末 Hebb学习规则
1958年 感知机
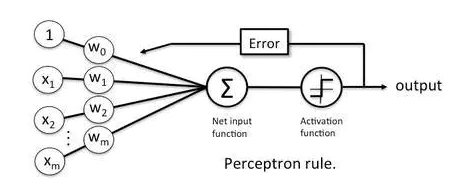
1969年 单层神经网络具有有限的功能
1974 年,Paul Werbos在哈佛大学攻读博士学位期间,就在其博士论文中发明了影响深远的著名BP神经网络学习算法
1982年,John Hopfield提出了连续和离散的Hopfield神经网络模型
1983年 玻尔兹曼机 隐藏单元
1986年 BP算法引入sigmod函数 克服训练的难题
1989年 BP神经网络的非线性函数逼近性能分析
—–神经网络由于其浅层结构,容易过拟合以及参数训练速度慢等淡化 10年—–
2006年GPU等硬件发展,BP算法迎来高光时刻

历史这样写就:从感知机提出,到BP算法应用以及2006年以前的历史被称为浅层学习,以后的历史被称为深度学习
BP算法先导知识
https://www.cnblogs.com/tangjunjun/articles/11649356.html
平方误差(西格玛)函数
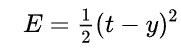
系数 1/2 是为了抵消微分出来的指数
归一化
min-max归一化
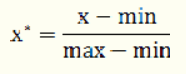
将一列数据变化到某个固定区间(范围)中,通常,这个区间是[0, 1]
导数
函数在该点的瞬时变化率
偏导数(round d)
函数在坐标轴方向上的变化率
方向导数
函数在某点沿某个特定方向的变化率
链式求导
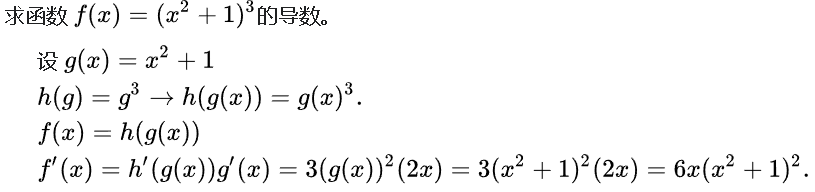
梯度
函数在该点沿所有方向变化率最大的那个方向
梯度下降
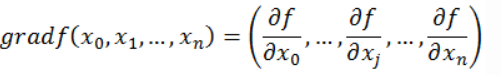
线性回归
数据使用线性预测函数来建模,并且未知的模型参数也是通过数据来估计
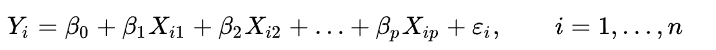
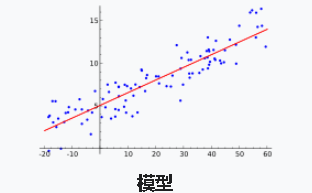
逻辑回归
主要解决二分类问题,用来表示某件事情发生的可能性
激活函数
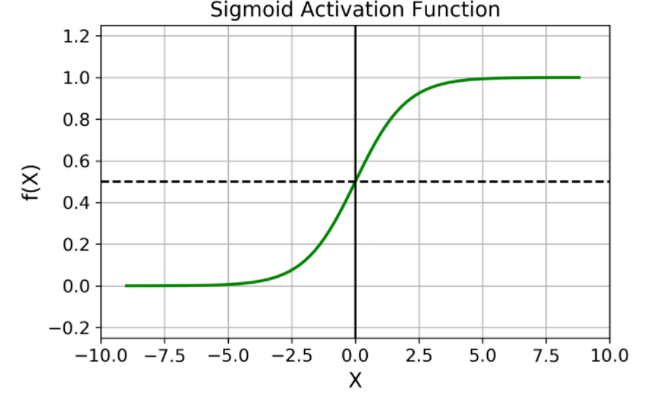
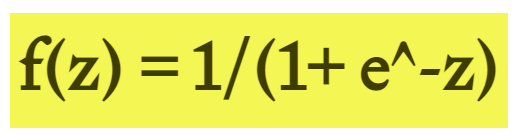
引入非线性函数作为激励函数,不再是输入的线性组合,而是几乎可以逼近任意函数
BP算法过程
https://www.cnblogs.com/duanhx/p/9655213.html
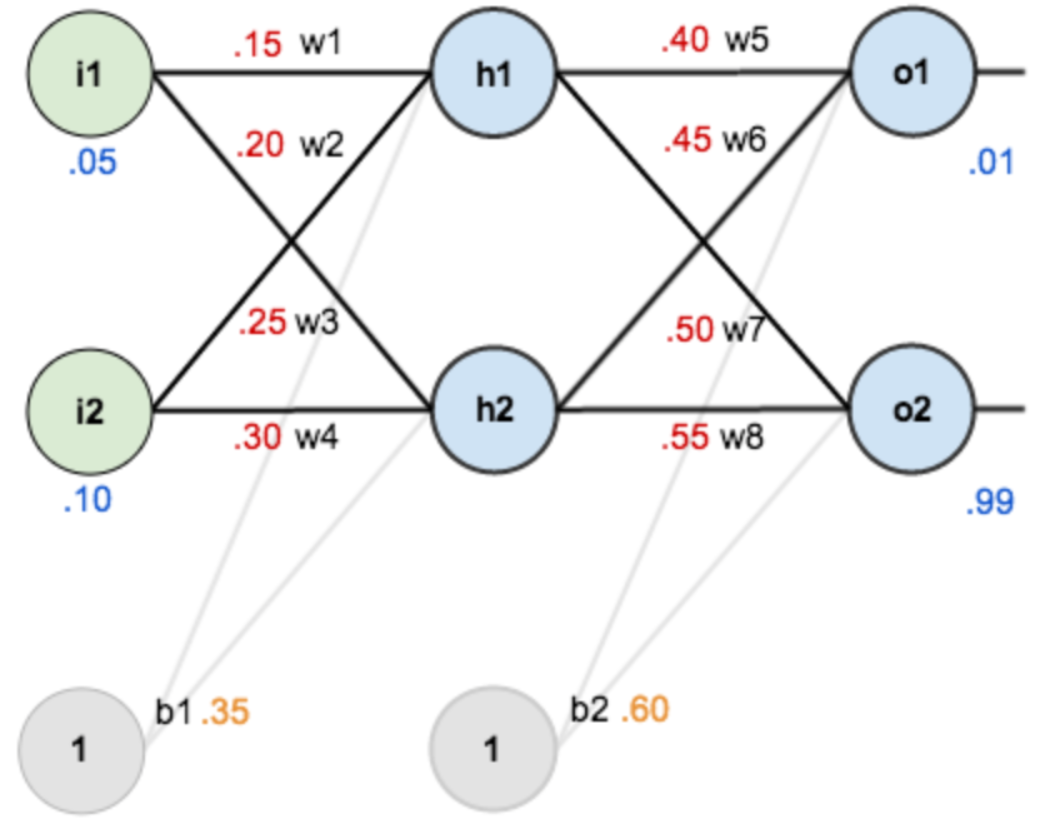
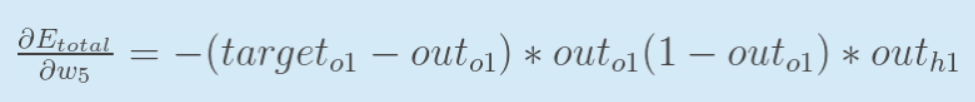
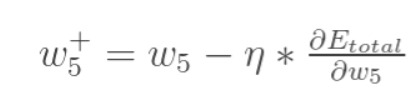
BP算法实现
步骤简述
- 数据归一化处理
- 设置初始权重
- 正向传播
- 反向计算误差
- 修正权重值
- 验证结果
三层网络算法(只有一个隐藏层)伪代码
初始化网络权值(通常是小的随机值)
do
forEach 训练样本 ex
prediction = neural-net-output(network, ex) // 正向传递
actual = teacher-output(ex)
计算输出单元的误差 (prediction - actual)
计算W(h)对于所有隐藏层到输出层的权值 // 反向传递
计算W(i)对于所有输入层到隐藏层的权值 // 继续反向传递
更新网络权值 // 输入层不会被误差估计改变
until 所有样本正确分类或满足其他停止标准
return 该网络